
Get ready for your data structures and algorithms course or exam with these 10 essential questions, diagrams, and code snippets. Learn about the most crucial concepts, algorithms, and data structures that every student should know.
Introduction: Are you a student preparing for a data structures and algorithms course or exam? Look no further! In this article, we've compiled the 10 most important DSA questions, along with diagrams and code snippets to help you ace your studies. These concepts are critical for any student pursuing a career in computer science or related fields, and mastering them will help you succeed in your coursework and beyond.Top10 Most Important Data Structures and Algorithms Questions for Students in Courses and Exams IQBug
A data structure is a way of organizing and storing data in a computer's memory, so that it can be accessed and processed efficiently. It is a fundamental concept in computer science and plays a critical role in programming and software development.
Data structures can be thought of as containers for storing and organizing data in a particular format. They provide a way to represent complex data in a simple and manageable way, making it easier to work with and manipulate the data.
In contrast, a data type is a classification of data based on the type of values that can be stored in a variable or a memory location. It defines the operations that can be performed on the data and the restrictions on its usage.
For example, in most programming languages, the integer data type can store whole numbers, such as -10, 0, or 100. The string data type, on the other hand, can store a sequence of characters, such as "hello world". Both data types define different types of data that can be stored, but they do not define how the data is stored in memory or how it can be manipulated.
Data structures, on the other hand, are used to store data in a particular format that is optimized for efficient access and manipulation. They can be classified into two main categories: linear and non-linear.
Linear data structures, such as arrays and linked lists, store data in a sequential manner. They allow for easy access to data elements and are useful for solving problems that require sequential processing.
Non-linear data structures, such as trees and graphs, store data in a hierarchical or networked manner. They allow for more complex relationships between data elements and are useful for solving problems that require more complex processing.
In summary, data structures are containers for storing and organizing data in a particular format that is optimized for efficient access and manipulation. Data types, on the other hand, are classifications of data based on the type of values that can be stored, and define the operations that can be performed on the data.
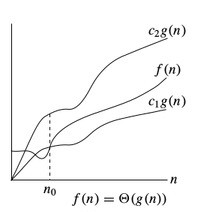
In computer science, time and space complexity are important measures that help us evaluate the performance of an algorithm. Time complexity refers to the amount of time required for an algorithm to execute, while space complexity refers to the amount of memory required by the algorithm.
Time complexity is usually expressed as a function of the input size. This means that as the input size increases, the time taken by the algorithm also increases. The notation used to express time complexity is called Big O notation, which provides an upper bound on the time taken by the algorithm. For example, if an algorithm has a time complexity of O(n), this means that the time taken by the algorithm grows linearly with the input size.
Space complexity, on the other hand, refers to the amount of memory required by an algorithm to execute. It is also expressed as a function of the input size. The space required by an algorithm can be affected by several factors, such as the data structures used by the algorithm, the size of the input data, and the number of variables used by the algorithm.
Analyzing an algorithm's time and space complexity is important for several reasons. Firstly, it helps us understand how an algorithm scales as the input size increases. This information can be used to determine whether an algorithm is suitable for a given problem or not. For example, an algorithm with a high time complexity may not be suitable for large datasets.
Secondly, analyzing an algorithm's complexity can help us identify performance bottlenecks in the code. By understanding which parts of the code are consuming the most time or memory, we can optimize the algorithm to make it more efficient.
Finally, understanding an algorithm's complexity can help us compare different algorithms and choose the one that is best suited for a given problem. By comparing the time and space complexity of different algorithms, we can determine which one is likely to provide the best performance for a given dataset.
In summary, time and space complexity are important measures that help us evaluate the performance of algorithms. Analyzing an algorithm's complexity allows us to understand how it scales as the input size increases, identify performance bottlenecks, and compare different algorithms to choose the most efficient one for a given problem.
Arrays and linked lists are two of the most fundamental data structures in computer science. While they have some similarities, they also have significant differences in terms of their implementation, advantages, and disadvantages.
Arrays are a type of data structure in which elements are stored sequentially in memory. Each element can be accessed using an index, which represents its position in the sequence. Arrays have a fixed size, which means that the number of elements they can store is determined at the time of creation. They are typically implemented as contiguous blocks of memory.
Linked lists, on the other hand, are a type of data structure in which elements are linked together using pointers. Each element, or node, contains a reference to the next element in the list. Linked lists can be either singly linked, meaning that each node contains a reference to the next node, or doubly linked, meaning that each node contains references to both the next and previous nodes.
One advantage of arrays is their fast access to elements using index. Because elements are stored sequentially in memory, the index of each element can be used to calculate its memory location quickly. This makes arrays an ideal choice for applications that require frequent access to individual elements, such as sorting and searching algorithms. Another advantage of arrays is that they have a fixed size, which means that the amount of memory required is known at the time of creation.
However, arrays also have some disadvantages. One major disadvantage is that their size is fixed, which means that they cannot be easily resized or modified. This can be problematic in situations where the number of elements to be stored is not known in advance. Additionally, because arrays are implemented as contiguous blocks of memory, inserting or deleting an element in the middle of an array requires shifting all the elements that come after it, which can be a time-consuming operation.
Linked lists have some advantages over arrays. One of the main advantages is that they can be easily resized and modified. Because each node contains a reference to the next (and previous) node, inserting or deleting an element requires only updating the pointers in the adjacent nodes, rather than shifting all the elements that come after it. This makes linked lists a good choice for applications that require frequent insertions and deletions.
However, linked lists also have some disadvantages. One major disadvantage is their slower access time to individual elements. Because elements are not stored sequentially in memory, accessing a particular element requires traversing the list from the beginning or end until the desired element is reached. This can be a time-consuming operation, especially for large lists. Another disadvantage is that linked lists require more memory than arrays because of the overhead associated with storing the pointers.
In summary, arrays and linked lists are both useful data structures, each with its own set of advantages and disadvantages. Arrays are ideal for applications that require frequent access to individual elements, while linked lists are better suited for applications that require frequent insertions and deletions. The choice of data structure depends on the specific requirements of the application and the tradeoffs between access time, memory usage, and ease of modification.
Recursion is a programming technique where a function calls itself within its body. Recursion is a powerful and versatile technique that can be used to solve many problems related to data structures.
The idea behind recursion is that a function can solve a problem by breaking it down into smaller subproblems that can be solved recursively. The function then combines the results of the subproblems to produce the final result.
Recursion can be used to traverse and search data structures such as trees and graphs. For example, a recursive function can be used to traverse a binary tree by recursively calling itself on the left and right subtrees. This allows the function to visit every node in the tree in a systematic and efficient manner.
Recursion can also be used to solve problems related to sorting and searching algorithms. For example, quicksort is a sorting algorithm that uses recursion to sort an array by recursively partitioning it into smaller subarrays. Each subarray is then sorted recursively until the entire array is sorted.
Another common use of recursion is to solve problems related to dynamic programming. Dynamic programming is a technique for solving problems by breaking them down into smaller subproblems and storing the results of the subproblems in a table. The results are then combined to solve the original problem. Recursion can be used to implement the subproblems by recursively calling the function and storing the results in a table.
One important aspect of recursion is the base case, which is the condition that stops the recursion. Without a base case, a recursive function will continue to call itself indefinitely, leading to a stack overflow error. The base case ensures that the function eventually terminates and returns a result.
Recursion can be a powerful tool in solving problems related to data structures. However, it can also be inefficient and lead to stack overflow errors if not implemented correctly. It is important to carefully design recursive functions and ensure that they have a base case and do not call themselves too many times.
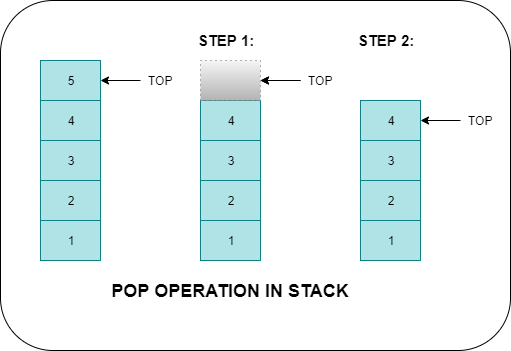
A stack is a linear data structure that operates on a Last-In-First-Out (LIFO) principle. In simple terms, it means that the element that is added last to the stack is the first one to be removed. The stack is a vital data structure used in many programming languages and is widely used in applications like expression evaluation, function call processing, and memory management.
A stack can be implemented using arrays or linked lists. The array implementation is relatively simple, and it consists of a fixed-size array where elements are pushed or popped from the top of the stack. The linked list implementation, on the other hand, consists of a set of nodes, where each node has two components: the data component and a pointer to the next node. The top of the stack is the head of the linked list, and elements are pushed or popped by adding or removing nodes at the head of the linked list.
There are three primary operations that can be performed on a stack: push, pop, and peek. Push is an operation that adds an element to the top of the stack. Pop is an operation that removes an element from the top of the stack. Peek is an operation that returns the element at the top of the stack without removing it.
The push operation is relatively simple, and it involves adding an element to the top of the stack. In the array implementation, this involves incrementing the index of the top element and adding the new element to the array. In the linked list implementation, a new node is added to the head of the linked list, and the pointer to the head is updated.
The pop operation is also straightforward and involves removing the top element from the stack. In the array implementation, this involves decrementing the index of the top element, and in the linked list implementation, the head node is removed, and the pointer to the head is updated.
The peek operation returns the element at the top of the stack without removing it. This operation is useful in many applications where we need to know the top element of the stack without removing it.
Apart from these basic operations, there are other operations that can be performed on a stack, such as checking if the stack is empty or full, and clearing the stack.
In conclusion, a stack is a fundamental data structure that is widely used in many programming applications. It is relatively simple to implement using arrays or linked lists and operates on a Last-In-First-Out principle. The three primary operations performed on a stack are push, pop, and peek, and there are additional operations like checking if the stack is empty or full and clearing the stack.
6. What is a queue? How is it implemented? Explain the various operations that can
be performed on a queue. Solution
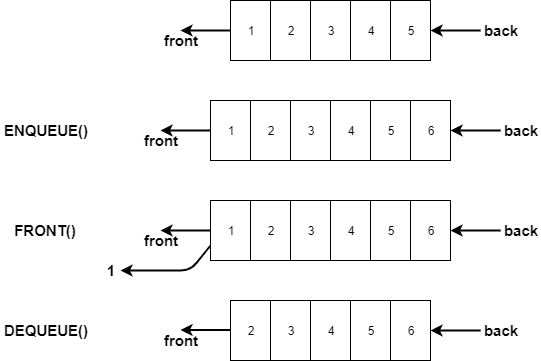
A queue is a linear data structure that follows the First In First Out (FIFO) principle. This means that the first element to be inserted into the queue is the first one to be removed. It is similar to a line of people waiting for their turn to be served, where the first person to arrive is the first to be served.
A queue can be implemented using an array or a linked list. In an array implementation, a fixed-size array is used to store the elements of the queue. A front and rear pointer are used to keep track of the elements in the queue. The front pointer points to the first element in the queue, while the rear pointer points to the last element in the queue. When an element is added to the queue, it is inserted at the rear end, and when an element is removed, it is removed from the front end.
In a linked list implementation, a linked list is used to store the elements of the queue. Each node in the linked list has two parts, a data part and a pointer part. The data part stores the element, while the pointer part points to the next element in the queue. A front and rear pointer are used to keep track of the elements in the queue, similar to the array implementation.
The various operations that can be performed on a queue are:
- Enqueue: This operation adds an element to the rear end of the queue. If the queue is full, it is called an overflow condition.
- Dequeue: This operation removes an element from the front end of the queue. If the queue is empty, it is called an underflow condition.
- Front: This operation returns the element at the front end of the queue without removing it.
- Rear: This operation returns the element at the rear end of the queue without removing it.
- Size: This operation returns the number of elements currently in the queue.
- IsEmpty: This operation checks if the queue is empty or not. If the queue is empty, it returns true, otherwise, it returns false.
Queues are used in various applications such as process scheduling, resource allocation, and in implementing algorithms like Breadth-First Search (BFS) in graph traversal. They can also be used to implement stacks, which is a data structure that follows the Last In First Out (LIFO) principle.
7. Explain the concept of a tree. What are the different types of trees? How are they
implemented? Solution
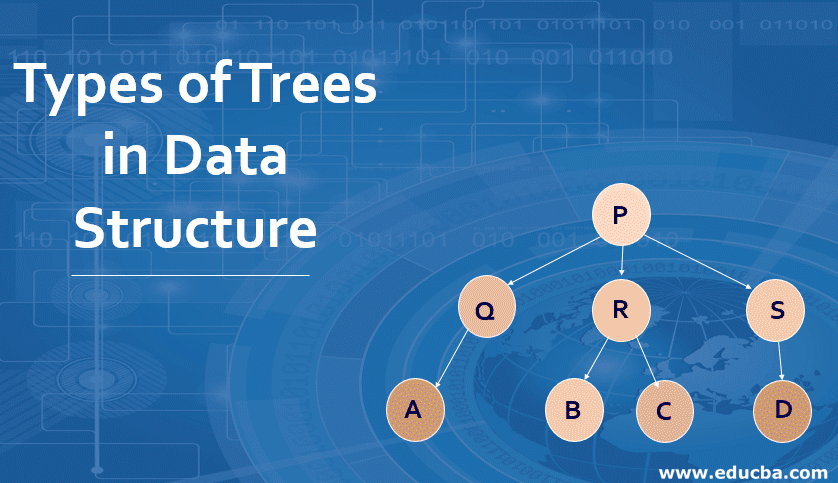
In computer science, a tree is a hierarchical data structure in which each node has a parent node and zero or more child nodes. The topmost node in a tree is called the root node, and the nodes with no children are called leaf nodes. Trees are commonly used to represent hierarchical structures such as file systems, organization charts, and family trees.
There are several types of trees, including:
Binary trees: A binary tree is a tree in which each node has at most two child nodes. It is commonly used to implement binary search trees, which allow efficient searching, insertion, and deletion of elements.
AVL trees: An AVL tree is a type of binary search tree that is self-balancing. It ensures that the difference in height between the left and right subtrees of any node is at most one, which guarantees that the height of the tree is logarithmic.
B-trees: A B-tree is a self-balancing tree data structure that can handle large amounts of data and is commonly used in databases and file systems. It allows efficient searching, insertion, and deletion of elements by maintaining a balance between depth and width.
Red-black trees: A red-black tree is another type of self-balancing binary search tree that ensures that the tree is approximately balanced. It is commonly used in Java's TreeMap and TreeSet classes.
Trees can be implemented using various data structures such as arrays, linked lists, and pointers. However, the most common implementation of trees uses nodes and pointers, where each node stores data and links to its child nodes. This implementation allows efficient traversal of the tree, insertion and deletion of nodes, and searching for specific nodes.
In conclusion, trees are a fundamental data structure used to represent hierarchical structures and provide efficient searching, insertion, and deletion operations. There are several types of trees, each with its own properties and use cases, and they can be implemented using different data structures depending on the requirements of the application.
8. What is a binary search tree? Explain its properties and operations that can be
performed on it.Solution
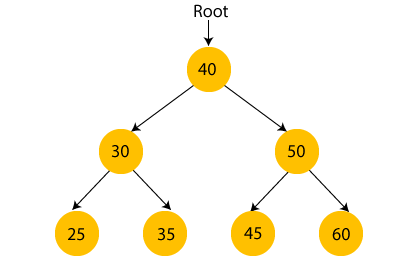
A binary search tree (BST) is a tree-based data structure in which each node has at most two children, and the value of the left child is less than the parent, while the value of the right child is greater.
The key properties of a BST are:
- The left subtree of a node contains only nodes with values less than the node's value.
- The right subtree of a node contains only nodes with values greater than the node's value.
- Both the left and right subtrees must also be binary search trees.
The most common operations that can be performed on a BST are:
Insertion: To insert a new node into the BST, the value of the node is compared with the value of the root node. If the value is less than the root, it is inserted in the left subtree; otherwise, it is inserted in the right subtree. This process is repeated recursively until a suitable leaf node is found.
Deletion: To delete a node from the BST, the node is first located, and then one of the following cases is handled:
- If the node has no children, it is simply removed.
- If the node has one child, the child replaces the node.
- If the node has two children, the node's successor (the minimum node in the right subtree) is found and replaces the node.
Searching: To search for a value in the BST, the value is compared with the value of the root node. If the value is less than the root, the search continues in the left subtree; otherwise, it continues in the right subtree. This process is repeated recursively until the value is found or the subtree is empty.
Traversal: BST can be traversed in three different ways:
- Inorder traversal: The left subtree is visited first, followed by the root node, and then the right subtree.
- Preorder traversal: The root node is visited first, followed by the left subtree, and then the right subtree.
- Postorder traversal: The left subtree is visited first, followed by the right subtree, and then the root node.
BSTs are efficient data structures for searching and sorting operations with a time complexity of O(log n), where n is the number of nodes in the tree. However, the worst-case time complexity of these operations can be O(n) if the tree is skewed. To avoid skewness, the tree can be balanced using techniques such as AVL trees or Red-Black trees.
9. Explain the concept of a graph. What are the different types of graphs? How are
they implemented?Solution
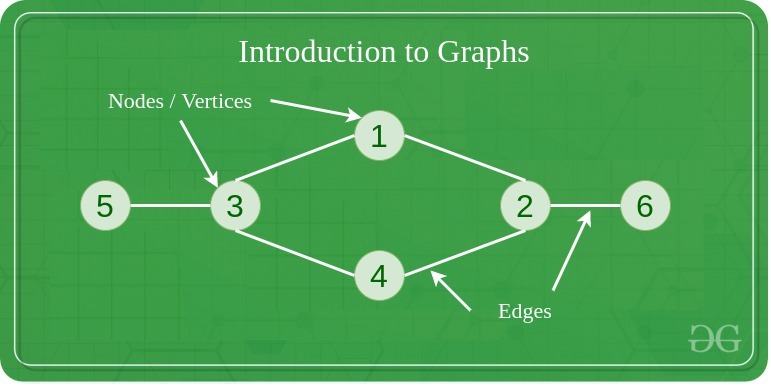
In computer science, a graph is a non-linear data structure consisting of a set of vertices or nodes connected by edges or links. Graphs are commonly used to model complex relationships and dependencies between objects in a system.
There are several types of graphs, including directed graphs, undirected graphs, weighted graphs, and unweighted graphs. In a directed graph, each edge has a direction, while in an undirected graph, edges have no direction. Weighted graphs have a value assigned to each edge, while unweighted graphs do not.
Graphs can be implemented using various data structures such as adjacency matrices and adjacency lists. An adjacency matrix is a two-dimensional array that stores the connections between vertices, while an adjacency list is a collection of linked lists that store the connections of each vertex.
Graphs are commonly used in various applications such as social networks, transportation networks, and computer networks. For example, social networks such as Facebook and LinkedIn use graphs to model relationships between users, while transportation networks use graphs to model connections between cities or airports.
Overall, graphs are a powerful tool for modeling complex relationships and dependencies in computer science, and their use can greatly improve the efficiency and effectiveness of various algorithms and systems.
10. What is the shortest path problem? How can it be solved using algorithms such
as Dijkstra's algorithm or the Bellman-Ford algorithm
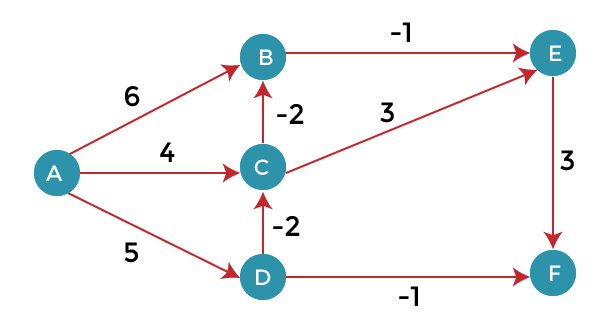
The shortest path problem is a common problem in computer science that involves finding the shortest path between two points in a graph. This problem is often encountered in routing applications, such as finding the shortest route between two cities or determining the fastest way to navigate through a network.
Dijkstra's algorithm is a popular algorithm for solving the shortest path problem in weighted graphs. It works by maintaining a set of vertices that have already been processed and a set of vertices that are yet to be processed. The algorithm selects the vertex with the shortest distance from the source vertex and updates the distances of its neighbors. This process is repeated until the destination vertex is reached or all vertices have been processed.
The Bellman-Ford algorithm is another algorithm that can be used to solve the shortest path problem. It works by initializing the distances of all vertices to infinity, except for the source vertex, whose distance is set to 0. The algorithm then iteratively updates the distances of all vertices by relaxing the edges in the graph. This process is repeated until no further updates can be made, or a negative-weight cycle is detected.
Both Dijkstra's algorithm and the Bellman-Ford algorithm have their advantages and disadvantages. Dijkstra's algorithm is generally faster than the Bellman-Ford algorithm in graphs with non-negative edge weights, but it does not work well in graphs with negative edge weights. On the other hand, the Bellman-Ford algorithm can handle graphs with negative edge weights, but it may be slower than Dijkstra's algorithm in some cases.
In conclusion, the shortest path problem is an important problem in computer science that can be solved using algorithms such as Dijkstra's algorithm and the Bellman-Ford algorithm. These algorithms have their strengths and weaknesses and can be applied in various applications where finding the shortest path is essential.
- most important questions data structures IQBug
- most important data structures and algorithms for interviews IQBug
- most important data structures and algorithms IQBug
- most important data structures and algorithms IQBug
Data structures and algorithms are fundamental concepts in computer science that every student must master. However, these concepts can be complex and challenging to understand, especially for beginners. This is where this essential guide comes in, providing a comprehensive overview of the 10 most important questions that students may encounter in their courses or exams.
The article is structured in a concise and easy-to-understand manner, making it accessible to students at all levels. It begins with an overview of the fundamentals of data structures and algorithms, providing a strong foundation for understanding the questions that follow. This includes an explanation of key concepts such as time and space complexity, recursion, and graph theory.
The article then delves into the 10 key questions, covering a wide range of topics including arrays, linked lists, trees, sorting algorithms, and more. Each question is presented in a clear and concise manner, with diagrams to illustrate key concepts and code snippets to demonstrate how to solve the problem. This approach makes it easy for students to grasp complex concepts and apply them to practical problems.
One of the key strengths of this article is that it includes tips and tricks for approaching each question. This is particularly useful for students who may be struggling with problem-solving skills. By following the practical examples provided in the article, students can build their problem-solving skills and prepare for their exams.
Overall, this article is an invaluable resource for students looking to excel in data structures and algorithms. It provides comprehensive coverage of key topics, clear explanations, and practical examples. Whether you are a beginner or an experienced programmer, this essential guide is sure to help you master these critical concepts and succeed in your studies


Comments